[备份] 用Java手写红黑树

介绍

二叉搜索树

二叉树：树的每个节点最多只能有两个子节点

二叉搜索树：

• 左子树不为空，左子树上所有节点的值均小于它的根节点的值
• 右子树不为空，右子树上所有节点的值均大于它的根节点的值

参考图片

查找：搜索值小于当前节点搜左子树，大于当前节点搜右子树，等于表示搜到 插入：类似查找，直到左子树或右子树为空时认为找到了插入位置

遍历：

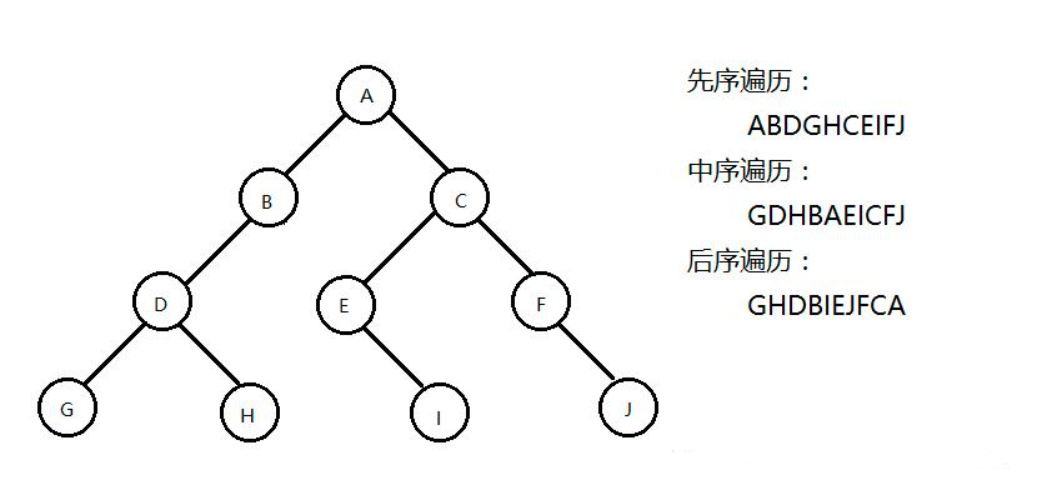
• 中序遍历：左-根-右（使用较多）
• 前序遍历：根-左-右
• 后序遍历：左-右-根

参考图片

最值：

• 最小值：最左边的节点
• 最大值：最右边的节点

删除：

• 叶节点：直接删（父节点指向空）
• 有一个子节点：由于二叉搜索树的特性，可以直接子承父位
• 有两个子节点：找到后继节点替换（大于该节点的最小节点）

二分查找

二分查找：数组有序情况下，对半查，参考下图

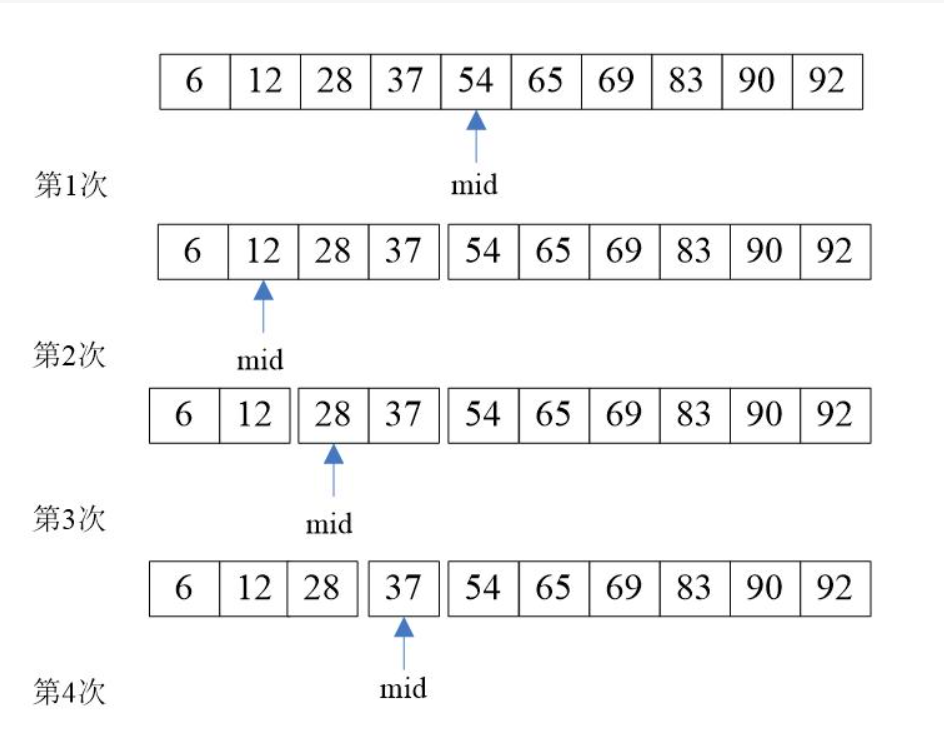
缺点：必须是有序的，而且是数组，不可以是链表

可以看出，二叉搜索树和二分查找有一定的相似度

AVL树

二叉搜索树存在一种极端情况，这种情况下会退化为一个有序链表

由于退化成链表后搜索效率过低，需要设计一种树，在插入元素的时候自动调整两边平衡，保持高查询性能。这里暂不分析AVL树，本节重点是红黑树

AVL树特点：

1. 具有二叉树全部特性
2. 左子树和右子树高度差最多是1
3. 插入或删除时，会涉及到左旋和右旋操作

虽然AVL树解决了二叉搜索树的极端情况，但是由于高度差限制过于严格，导致效率过低

于是引出了红黑树的概念

基础

性质

红黑树具有以下的性质，如果满足那么这棵树就是趋于平衡状态的：

• 每个节点是黑色或红色
• 根节点是黑色
• 叶节点是黑色
• 每个红色节点的两个子节点是黑色，红色节点不能相连
• 任意节点到每个叶节点的路径都包含相同的黑节点，又称黑高
• 如果一个节点存在黑子节点，那么该节点一定有两个子节点

自平衡

1. 变色：节点颜色红黑变化
2. 左旋：某节点右子节点变成父节点，右子节点的左节点变为它的右节点，左子节点保持不变
3. 右旋：某节点左子节点变成父节点，左子节点的右节点变为它的左节点，右子节点保持不变

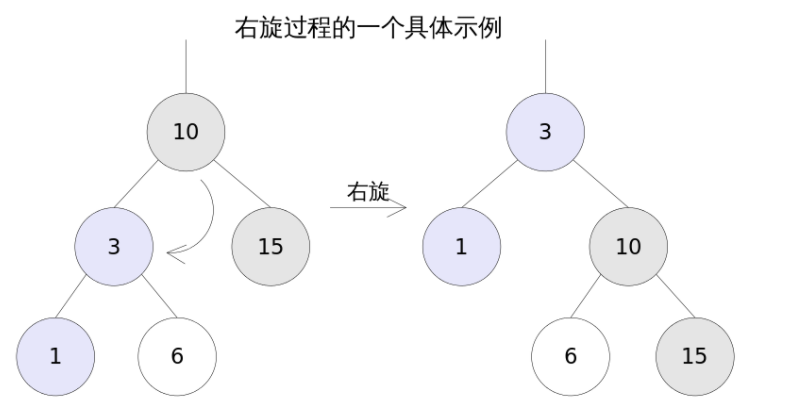
实现

红黑树的插入等操作会涉及到多种情况，暂不分析，直接上代码，在代码中分析

树节点

xxxxxxxxxx
// 树节点
static class RBNode<K extends Comparable<K>, V> {
    private RBNode parent;
    private RBNode left;
    private RBNode right;
    private boolean color;

    private K key;
    private V value;

    // 构造 get set
    // ......
}

左旋实现

xxxxxxxxxx
/**
* 左旋
*      p              p
*      |              |
*      x              y
*     / \   --->     / \
*    lx  y          x   ry
*   / \            / \
*  ly ry          lx ly
*
* (1) x.right=y.left
* (2) y.left.parent=x
* (3) y.parent=x.parent
* (4) x.parent=y
*
* @param x 左旋节点
*/
private void leftRotate(RBNode x) {
    RBNode y = x.right;
    // (1)
    x.right = y.left;
    // (2)
    if (y.left != null) {
        y.left.parent = x;
    }
    // (3)
    if (x.parent != null) {
        y.parent = x.parent;
        if (x == x.parent.left) {
            x.parent.left = y;
        } else {
            x.parent.right = y;
        }
    } else {
        // root
        this.root = y;
    }
    // (4)
    x.parent = y;
    y.left = x;
}

右旋实现

xxxxxxxxxx
/**
* 右旋
*      p              p
*      |              |
*      y              x
*     / \   --->     / \
*    x  ry          lx  y
*   / \                / \
*  lx ly              ly ry
*
* (1) y.left=x.right
* (2) x.right.parent=y
* (3) x.parent=y.parent
* (4) y.parent=x
*
* @param y 右旋节点
*/
private void rightRotate(RBNode y) {
    RBNode x = y.left;
    // (1)
    y.left = x.right;
    // (2)
    if (x.right != null) {
        x.right.parent = y;
    }
    // (3)
    if (y.parent != null) {
        x.parent = y.parent;
        if (y == y.parent.left) {
            y.parent.left = x;
        } else {
            y.parent.right = x;
        }
    } else {
        // root
        this.root = x;
        this.root.parent = null;
    }
    // (4)
    y.parent = x;
    x.right = y;
}

插入

xxxxxxxxxx
/**
* 对外的插入
* @param key key
* @param value value
*/
public void insert(K key, V value) {
    RBNode node = new RBNode();
    node.setKey(key);
    node.setValue(value);
    // 新节点一定是红色
    node.setColor(RED);
    insert(node);
}

/**
* 插入实现
* @param node 插入节点
*/
private void insert(RBNode node) {
    RBNode parent = null;
    RBNode x = this.root;

    while (x != null) {
        parent = x;
        // cmp>0:node.key>x.key->遍历右子树
        // cmp=0:node.key=x.key->replace
        // cmp<0:node.key<x.key->遍历左子树
        int cmp = node.key.compareTo(x.key);
        if (cmp > 0) {
            x = x.right;
        } else if (cmp == 0) {
            x.setValue(node.getValue());
            return;
        } else {
            x = x.left;
        }
    }
    node.parent = parent;
    if (parent != null) {
        // cmp>0:node.key>parent.key->node在parent右子节点
        // cmp<0:node.key<parent.key->node在parent左子节点
        int cmp = node.key.compareTo(parent.key);
        if (cmp > 0) {
            parent.right = node;
        } else {
            parent.left = node;
        }
    } else {
        this.root = node;
    }

    // 恢复平衡
    insertFixup(node);
}

恢复平衡

xxxxxxxxxx
private void insertFixup(RBNode node) {
    this.root.setColor(BLACK);
    // 父节点
    RBNode parent = parentOf(node);
    // 父节点的父节点
    RBNode gparent = parentOf(parent);
    // 父节点为黑色直接平衡
    // 父节点为红色应分多种情况
    if (parent != null && isRed(parent)) {
        // 父节点的父节点的另一个子节点（叔叔）
        RBNode uncle = null;
        // 父节点是爷节点左节点
        if (parent == gparent.left) {
            uncle = gparent.right;
            /**
            *         |                      |
            *      gp(B)                   gp(R)
            *      /   \      --->         /   \
            *    p(R)  u(R)              p(B)  u(B)
            *    /                       /
            *  n(R)                    n(R)
            */
            if (uncle != null && isRed(uncle)) {
                // 重新染色后下一轮处理
                setBlack(parent);
                setBlack(uncle);
                setRed(gparent);
                insertFixup(gparent);
                return;
            }
            if (uncle == null || isBlack(uncle)) {
                /**
                *         |                      |
                *      gp(B)                    p(B)
                *      /   \      --->         /   \
                *    p(R)  u(B)              n(R)  gp(R)
                *    /                               \
                *  n(R)                              u(B)
                */
                if (node == parent.left) {
                    setBlack(parent);
                    setRed(gparent);
                    // 右旋
                    rightRotate(gparent);
                    return;
                }
                /**
                *         |                      |
                *      gp(B)                    gp(B)
                *      /   \      --->         /   \       ---> 上一步
                *    p(R)  u(B)              n(R)  u(B)
                *       \                    /
                *       n(R)               p(R)
                */
                if (node == parent.right) {
                    leftRotate(parent);
                    insertFixup(parent);
                    // 右旋
                    return;
                }
            }
        } else {
            // 父节点是右节点
            uncle = gparent.left;
            /**
            *         |                      |
            *      gp(B)                   gp(R)
            *      /   \      --->         /   \
            *    u(R)  p(R)              u(B)  p(B)
            *    /                       /
            *  n(R)                    n(R)
            */
            if (uncle != null && isRed(uncle)) {
                // 重新染色后下一轮处理
                setBlack(parent);
                setBlack(uncle);
                setRed(gparent);
                insertFixup(gparent);
                return;
            }
            // 不存在叔节点
            if (uncle == null || isBlack(uncle)) {
                /**
                *         |                      |
                *      gp(B)                    p(B)
                *      /   \      --->         /   \
                *    u(B)  p(R)              gp(R) n(R)
                *            \               /
                *            n(R)          u(R)
                */
                if (node == parent.right) {
                    setBlack(parent);
                    setRed(gparent);
                    leftRotate(gparent);
                    return;
                }
                /**
                *         |                      |
                *      gp(B)                    gp(B)
                *      /   \      --->         /   \     ---> 上一步
                *    u(B)  p(R)              u(B)  n(R)
                *          /                         \
                *        n(R)                        p(R)
                */
                if (node == parent.left) {
                    rightRotate(parent);
                    insertFixup(parent);
                    return;
                }
            }
        }
    }
}